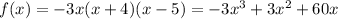Question

Find an expression for a cubic function f if f(4) = 96 and f(-4) = f(0) = f(5) = 0. Part 1 of 4 A cubic function generally has the form f(x) = ax3 + bx2 + cx + d. If we know that for some x-value x = p we have f(p) = 0, then it must be true that x − p is a factor of f(x). Since we are told that f(5) = 0, we know that x-5 Correct: Your answer is correct. seenKey x-5 is a factor. Part 2 of 4 Similarly, since f(−4) = 0, then f(x) has the factor x+4 Correct: Your answer is correct. seenKey x+4 , and since f(0) = 0, then f(x) has the factor x Correct: Your answer is correct. seenKey x .

Answer 1

Given a polynomial
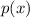`p(x)` and a point
`x_0`, we have that

`p(x_0) = 0 \iff (x-x_0) \text{\ divides\ } p(x)`

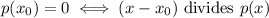
We know that our cubic function is zero at -4, 0 and 5, which means that our polynomial is a multiple of

`(x+4)(x)(x-5) = x(x+4)(x-5)`

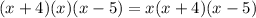
Since this is already a cubic polynomial (it's the product of 3 polynomials with degree one), we can only adjust a multiplicative factor: our function must be

`f(x) = ax(x+4)(x-5),\quad a \in \mathbb{R}`

To fix the correct value for a, we impose
`f(4)=96`:

`f(4) = 4a(4+4)(4-5) = -32a = 96`

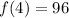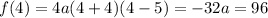
And so we must impose

`-32a=96 \iff a = -(96)/(32) = -3`

So, the function we're looking for is

`f(x) = -3x(x+4)(x-5)=-3x^3+3x^2+60x`