Question

"A bullet is fired horizontally with speed vi = 400.0m/s at the bullseye (from the same level). The bullseye is a horizontal distance x = 100.0m away. Since the bullet will fall under gravity, it will miss the bullseye. By what vertical distance does the bullet miss the bullseye?At what angle above the horizontal should the bullet be fired to successfully hit the target? Your bullet is aimed at a target (along the line). The target is released the instant the bullet is fired. Can you hit the target?"

Answer 1

It will miss the target of bulls eye by 0.30625 m

The bullet should make an angler of
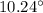`10.24^\circ` with the horizontal in order to hit the target.

Step-by-step explanation:

Given:

• Initial speed of the bullet .
  `v_i=400\ \rm m/s`
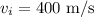
• The horizontal distance of the target., x=100 m

Since the bullet is fired horizontally. Let y be the vertical distance by which the it will miss the target

Now equation of motion

`x=v_it\\y=(gt^2)/(2)\\`

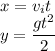
Substituting the value of t we have

`y=(gx^2)/(2u^2)\\y=(9.8*100^2)/(2*400^2)\\\\y=0.30625\ \rm m`

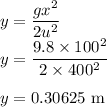
Now let
`\theta` bet he angle with horizontal that it is making t hit the target. The bullet is initially at the same height as that of target in order to hit the target the vertical displacement of the bullet should be zero.

`y=x\tan\theta-(gx^2)/(2u^2g(cos\theta)^2)\\0=100* tan\theta-(9.8* 100^2)/(2*400^2 (\cos\theta)^2)\\\theta=10.24^\circ`

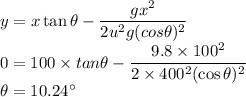
When the bullet is aimed at the target and the target is released at the same instant the bullet is fired then it will hit the target.