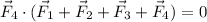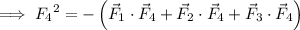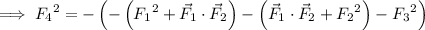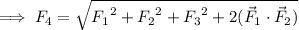We want to find
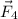 such that the object needs is in equilibrium:
such that the object needs is in equilibrium:
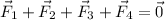
We're told that
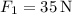 ,
,
 , and
, and
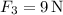 . We also know the angle between
. We also know the angle between
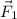 and
and
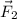 is 95º, which means
is 95º, which means
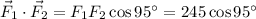
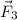 is perpendicular to both
is perpendicular to both
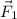 and
and
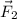 , so
, so
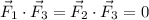 .
.
If we take the dot product of
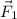 with the sum of all four vectors, we get
with the sum of all four vectors, we get
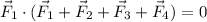
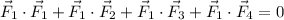
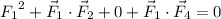
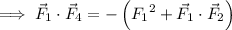
We can do the same thing with
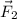 and
and
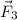 :
:
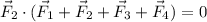
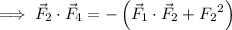
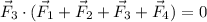
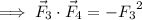
Finally, if we do this with
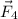 , we get
, we get