Answer: 0.0034
Explanation:
Given : The distribution of SAT scores (combining mathematics and reading) was approximately Normal with
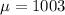 and
and

let x be the random variable that represents the SAT scores.
Using formula
 , the value of z corresponding to 1600 will be :-
, the value of z corresponding to 1600 will be :-
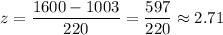
By using the standard normal table , we have
The proportion of SAT scores were actually higher than 1600 will be :-
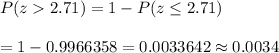
Hence, the proportion of SAT scores for the combined portions were reported as 1600 = 0.0034