Question

Two charges are located in the xx – yy plane. If ????1=−4.25 nCq1=−4.25 nC and is located at (x=0.00 m,y=1.080 m)(x=0.00 m,y=1.080 m) , and the second charge has magnitude of ????2=3.80 nCq2=3.80 nC and is located at (x=1.30 m,y=0.450 m)(x=1.30 m,y=0.450 m) , calculate the xx and yy components, ????xEx and ????yEy , of the electric field, ????⃗ E→ , in component form at the origin, (0,0)(0,0) . The Coulomb force constant is 1/(4????????0)=8.99×109 N⋅m2/C21/(4πϵ0)=8.99×109 N⋅m2/C2 .

Answer 1

Ex= -17.1 N/C

Ey = +26.9 N/C

Step-by-step explanation:

We apply formula of electric field:

Ep=k*q/d²

Ep: Electric field at point ( N/C)

q: Electric charge (C)

k: coulomb constant (N.m²/C²)

d: distance from charge q to point P (m)

In the attached graph we observe the directions of the electric field at P(0,0) due to q1 and q2

Calculation of the field at point P due to the load q₁

E₁=k*q₁/d₁² = 9*10⁹*4.25*10⁻⁹/1.080²= 32.8 N/C : Magnitude of E1

Direction of E₁ :Because the charge q₁ is negative the field enters the charge (+ y)

Calculation of the field at point P due to the load q₂

`d_(2) = \sqrt{1.30^(2)+0.450^(2)  }`

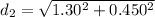
d₂=1.375 m

E₂=k*q₂/d₂² = 9*10⁹*3.80*10⁻⁹/ 1.375² = 18.09 N/C Magnitude of E₂

Direction of E₂ :Because the charge q₂ is positive the field leaves the charge in direction of angle β

, then,E₂ tiene componentes x-y en P.

E₂x=-E₂cos β= -18.09*(1.3/1.375)= -17.1 N/C

E₂y=-E₂sin β= -18.09*(0.45/1.375)= -5.9 N/C

Calculation of the electric field at point P located at the origin(0,0)

Ex=E₂x= -17.1 N/C

Ey=E₁y+E₂y =32.8 N/C -5.9 N/C = 26.9 N/C