Question

Two children own two-way radios that have a maximum range of 3 miles. One leaves a certain point at 1:00 P.M., walking due north at a rate of 6 mi/hr. The other leaves the same point at 1:15 P.M., traveling due south at 9 mi/hr. For how many minutes after 1:00 P.M. will they be able to communicate with one another? (Round your answer to the nearest minute.)

Answer 1

The answer is 21 minutes

Explanation:

We use the equation Xf = Xo + vt

1) At 1:00 PM, child one leaves the starting point heading north at a constant velocity of 6 mi/hr or .1 [mi/min] (divide by 60 to convert from [mi/hr] to [mi/min])

2) He walks for 15 minutes before kid 2 starts walking. In 15 minutes he is able to cover 1.5 [mi]

• 
  `x_(1f1) =x_(o) +v_(1) t_(1) \\x_(1f1) =0+.1(15)\\x_(1f1) =1.5 [mi]`

3) Now, child 2 starts walking and we know that when the range reaches 3 miles, they won´t be able to communicate. So the sum of the final position of child 1 and child 2 must be 3[mi]

• Child 1 final position =>
  `x_(1f) = x_(1f1) +v_(1) t\\x_(1f) =1.5+v_(1) t`
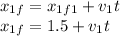
• Child 2 final position =>
  `x_(2f) =0+v_(2) t`

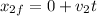
4) Sum the equations and equate to 3

• 
  `x_(1f) +x_(2f) =3`

5) Substitute the values we already know

• 
  `1.5+v_(1) t+v_(2)t=3\\ 1.5+.1t+.15t=3\\1.5+.25t=3\\t=(3-1.5)/(.25) \\t=6 [min]`

6) in 15 + 6 minutes they will be 3miles apart

7) In 21 minutes they will still be able to communicate with one another.