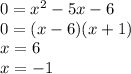Question

I need help bruv. For the function y=x^2 - 5x - 6 .

(a) Find the vertex


(b) Find the y-intercept


(c) Find the x-intercepts


(Leave your answers in simplified radical form or, where appropriate, round to the nearest hundredth.)

Answer 1

a. Vertex = (2.5,-12.25)

b. y-intercept = (0,-6)

c. x-intercept = (6,0) ; (-1,0)

Explanation:

a.

Your equation is written as:

`y = ax^(2) + bx +c`

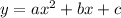
The easiest way to find the vertex is writing the equation this way:

`y = a(x-h)^(2)+k`

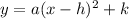
Being the vertex (h,k)

So first complete the square

`y = x^(2) -5x -6 \\y = x^(2) - 2(2.5x) -6 \\y = x^(2) - 2(2.5x) +2.5^(2) - 2.5^(2) -6 \\y = (x^(2) -2(2.5x) + 2.5^(2)) -6.25 - 6 \\y = (x-2.5)^(2) -12.25`

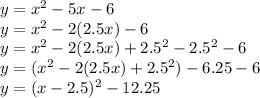
Vertex : (2.5,-12.25)

b.

To find the y-intercept you need to replace the equation when x = 0 and get y

`y = (0)^(2) - 5(0) -6\\y = - 6`

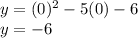
c.

To find the x-intercept you need to replace the equation when y = 0 and get x

`0 = x^(2) - 5x -6 \\0 = (x-6)(x+1)\\x = 6\\x = -1`