Question

Suppose that 55% of all adults regularly consume coffee, 45% regularly consume carbonated soda, and 70% regularly consume at least one of these two products. a. What is the probability that a randomly selected adult regularly consumes both coffee and soda? b. What is the probability that a randomly selected adult doesn’t regularly consume at least one of these t

Answer 1

a. The probability that an adult regularly consumes both coffee and soda is 0.30

b. The probability that an adult does not consume at least one of the two drinks is 0.70

Explanation:

Let the events be:

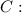`C:` The adult consumes coffee regularly.

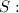`S:` The adult consumes soda regularly.

`P(C)=0.55\\\\P(S)=0.45\\\\P(C\bigcup S)=0.70`

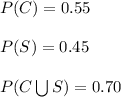
The additive rule to calculate probabilities of non-disjoint events states that:

`P(C\bigcup S)=P(C)+P(S)-P(C\bigcap S)`

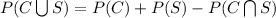
Thus,

`P(C\bigcap S)=P(C)+P(S)-P(C\bigcup S)`

`P(C\bigcap S)=0.55+0.45-0.70=0.30`

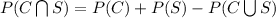
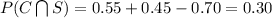
The probability that an adult regularly consumes both coffee and soda is 0.30

Applying the complement property, you have to

`P(C'\bigcup S')=1-P(C\bigcap S)`

`P(C'\bigcup S')=1-0.3=0.70`

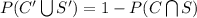
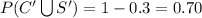
The probability that an adult does not consume at least one of the two drinks is 0.70