Answer:
Explanation:
15) point D=(3,1)
for AB we can see that there is an exact triangle of 2 and 5
so AD =
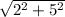 =
=
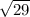 and 2(AD) = AB
and 2(AD) = AB
AB = 2*
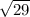 ( this is an exact answer, leave it with the square root)
( this is an exact answer, leave it with the square root)
16) find CD length we know the points at each end so use the distance formula P1=(-3,4) P2=(3,1)
Dist. =
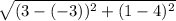
Dist. =
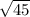 =
=
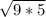 = 3
= 3
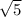 ( exact answer leave the square root )
( exact answer leave the square root )
CD = 3
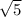
17) 1/3 of the way along CD from D towards C is where the centroid is.. I just happen to know that from doing this too often. :/
so that mean
 *
*
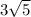 is the distance from D to the centroid or
is the distance from D to the centroid or
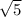
also b/c I happen to know.. :/ c =
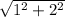 =
=
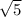 off the top of my head I can see that the point (1,2) is our centroid for this object.. they made it really easy ... okay.. relatively easy. .:D
off the top of my head I can see that the point (1,2) is our centroid for this object.. they made it really easy ... okay.. relatively easy. .:D
Centroid = (1,2)