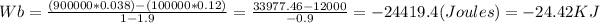Question

A gas in a piston–cylinder assembly undergoes a process for which the relationship between pressure and volume is pVn = constant. The initial pressure is 1 bar, the initial volume is 0.12 m3, and the final pressure is 9 bar. The value of the polytropic exponent is n = 1.9. Determine the final volume, in m3, and the work for the process, in kJ.

Answer 1

The final volume is: 0.038 m3 adn the work for the process is: -24.42 KJ

Step-by-step explanation:

The equation given for a polytropic process
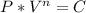`P*V^(n)=C` when n and C are constants. First we determine the C with the initial conditions:
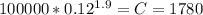`100000*0.12^(1.9)=C= 1780`, we need to remember that 1 bar is the same to 100000 Pascals. Then we can calculate the final volume solving the equation given to:
`Vfinal=\sqrt[n]{(C)/(Pfinal)}` so we get:
`Vfinal=\sqrt[1.9]{(1780)/(900000) } = 0.038(m3)`. Now using the integration for work:
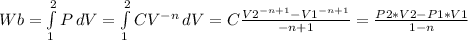`Wb=\int\limits^2_1 {P}\,dV=\int\limits^2_1 {CV^(-n) } \, dV=C(V2^(-n+1)-V1^(-n+1))/(-n+1) =(P2*V2-P1*V1)/(1-n)`, replacing data we find the work process like:
`Wb=((900000*0.038)-(100000*0.12))/(1-1.9) =(33977.46-12000)/(-0.9) =-24419.4 (Joules)=-24.42 KJ`