Answer:
See explanation
Step-by-step explanation:
You are given the equation of the curve
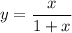
Point
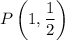 lies on the curve.
lies on the curve.
Point
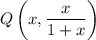 is an arbitrary point on the curve.
is an arbitrary point on the curve.
The slope of the secant line PQ is
![(y_2-y_1)/(x_2-x_1)=((x)/(1+x)-(1)/(2))/(x-1)=((2x-(1+x))/(2(x+1)))/(x-1)=((2x-1-x)/(2(x+1)))/(x-1)=\\ \\=((x-1)/(2(x+1)))/(x-1)=(x-1)/(2(x+1))\cdot (1)/(x-1)=(1)/(2(x+1))\ [\text{When}\ x\\eq 1]](https://img.qammunity.org/2020/formulas/mathematics/high-school/uwt84o2sxdjikp6m2qlq0f0ex824a5k2s7.png)
1. If x=0.5, then the slope is
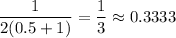
2. If x=0.9, then the slope is
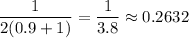
3. If x=0.99, then the slope is
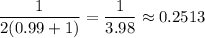
4. If x=0.999, then the slope is
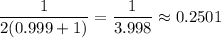
5. If x=1.5, then the slope is
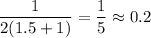
6. If x=1.1, then the slope is

7. If x=1.01, then the slope is
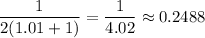
8. If x=1.001, then the slope is
