Question

A​ pitcher's earned-run average E varies directly as the number R of earned runs allowed and inversely as the number I of innings pitched. A certain pitcher had an​ earned-run average of​ 2.92, giving up 85 earned runs in 262 innings. How many earned runs would the pitcher have given up having pitched 330 innings with the same​ average?

Answer 1

The pitcher would have 107 earned runs

Explanation:

- The earned-run average is E

- The number of earned runs is R

- The number of innings pitched is I

- E varies directly with R ⇒ E ∝ R

- E is varies inversely with I ⇒ E ∝
`(1)/(I)`

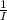
- The earned average is 2.92 when giving up 85 earned runs in

262 innings

- We need to find how many earned runs would the pitcher have given

up having pitched 330 innings with the same​ average

∵ E ∝ R and E ∝
`(1)/(I)`

∴
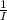
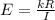`E=(kR)/(I)` , where k is the constant of variation

- To find the constant of variation k we must use the initial values of E,

R, and I

∵ E = 2.92 , R = 85 and I = 262

- Substitute these values in the equation above

∴
`2.92=(k(85))/(262)`

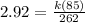
- Multiply both sides by 262

∴ 765.04 = 85 k

- Divide both sides by 85

∴ k ≅ 9

- Substitute the value of k in the equation

∴ The equation is
`E=(9R)/(I)`

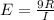
∵ E = 2.92 (same average)

∵ I = 330 innings

- We need to find the number of earned runs R

∴
`2.92=(9R)/(330)`

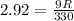
- Multiply both sides by 330

∴ 963.6 = 9 R

- Divide both sides by 9

∴ R = 107.07 ≅ 107

* The pitcher would have 107 earned runs