Answer:
The equation that gives the price p they can charge for n shirts is
p = -0.005n + 82
Step-by-step explanation:
Establish the variables for the equation
n = number of shirts that can sell
p = price per shirt
For case one we have n1 = 5000 p1 =$57
For case two we have n2 = 15000 p2= $7
Calculate the slope remeber that
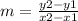 in this case the y will be represented by the price (p) and the x by the number (n) so we have:
in this case the y will be represented by the price (p) and the x by the number (n) so we have:
m =
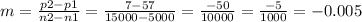
Replace in the equation (y-y1) = m (x - x1) with our variables:
(p-p1) = m(n-n1)
p - 57 = -0.005 (n - 5000)
p - 57 = -0.005n + 25
p = -0.005n + 25 + 57
p = -0.005n + 82
To verify we can replace for example the values of n2 to get p2 as follows
p= -0.005 (15000) + 82
p = - 75 + 82
p = 7
If fulfills the condition that for 15000 shirts the price is $ then the equation is correct