Question

A drowsy cat spots a flowerpot that sails first up and then down past an open window. The pot is in view for a total of 0.66 s, and the top-to-bottom height of the window is 1.80 m. How high above the window top does the flowerpot go? (Assume that in both sailing upward and then falling downward, the flowerpot is seen to span the full vertical height of the window.)

Answer 1

Height covered after crossing window top = 0.75 m

Explanation:

In the question,

The height of the window pane = 1.8 m

Time for which the flowerpot is in view = 0.66 s

So,

The time for which it was in view while going up is = 0.33 s

Time for which it was in view while going down = 0.33 s

So,

Let us say,

The initial velocity of the flowerpot = u m/s

So,

Using the equation of the motion,

`s=ut+(1)/(2)at^(2)\\1.8=u(0.33)-(1)/(2)(9.8)(0.33)^(2)\\1.8=0.33u-0.5336\\0.33u=2.33\\u=7.07\,m/s`

So,

Velocity at the top of the window pane is given by,

`v=u+at\\v=7.07-(9.8)(0.33)\\v=3.836\,m/s`

Now,

Let us say the height to which the flowerpot goes after crossing the window pane is = h

So,

Using the equation of motion,

`v^(2)-u^(2)=2as\\(0)^(2)-(3.836)^(2)=2(-9.8)h\\h=(14.714)/(19.6)\\h=0.75\,m`

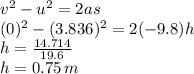
Therefore, the height covered by the flowerpot after window is = 0.75 m