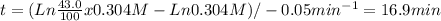Question

The decomposition of A to B is a first-order reaction with a half-life of 14.2 min: A → 2B If the initial concentration of A is 0.304 M, how long will it take for the concentration of A to decrease by 43.0 %?

Answer 1

It take 16.9 min for the concentration of A to decrease by 43.0 %

Step-by-step explanation:

The first-order reaction law is
`Ln [A] = -k.t + Ln [A]_(0)`

And the half-life time for the first-order reaction is
`t_(1/2) =(Ln 2)/(k)`

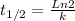
- [A] is the concentration of the reactant at any time (t) of the reaction

- [A]0 is the concentration of the reactant at the beginning of the reaction

- k is the rate constant.

- t1/2 is the half-life time

Thus, for this reaction k is

`k = (Ln 2)/(t_(1/2))  = (Ln 2)/(14.2min) = 0.05 min^(-1)`

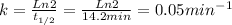
Decreasing the concentration of the reactant by 43.0% means the concentration of A (reactant) at the end of the reaction has to be:

`[A] = (43.0)/(100)x[A]_(0)`

Replacing [A] in the equation of the law

`Ln (43.0)/(100) [A]_(0) = -k.t + Ln [A]_(0)`

Clearing the t

`(Ln (43.0)/(100) [A]_(0) - Ln [A]_(0) ) / -k = t`

Replaicing with [A]0 = 0.304M and k = 0.05min-1

`t = (Ln (43.0)/(100)x0.304M - Ln 0.304M ) / -0.05 min^(-1) = 16.9 min`