Question

One-fourth of the residents of a particular community leave their garage doors unlocked when they go out to do an errand. The local chief of police estimates that 5 percent of the garages with the doors unlocked will have something stolen, but only 1 percent of those locked will have something stolen. What is the probability if a garage is selected at random it will be unlocked? Express your answer as a decimal carried out two places, e.g .10.

Answer 1

Required Probability = 0.625

Explanation:

Given,

Probability of unlocked doors, P(U) = 0.25

Probability of locked doors, P(U') = 0.75

Probability of something being stolen when door is unlocked, P(S/U) = 0.05

Probability of something not being stolen when door is unlocked, P(S'/U) = 0.95

Probability of something being stolen when door is locked, P(S/U') = 0.01

Probability of something not being stolen when door is locked, P(S'/U') = 0.99\

probability of being stolen either door is locked or not,

P(S) =P(S/U).P(U) + P(S\U').P(U')

= 0.05 x 0.25 + 0.95 x 0.75

= 0.0125 + 0.0075

= 0.02

Probability that door was unlocked when while steeling can by given by

`P(U/S)\ =\ (P(S/U).P(U))/(P(S))`

`=\ (0.05* 0.25)/(0.02)`

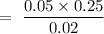
= 0.625

hence, the required probability is 0.625.