Question

Two runners start at the same point on a straight track. The first runs with constant acceleration so that he covers 98 yards in 10 seconds. The second runner waited 5 seconds and then throws a rock at his opponent's head. Of the head and the rock are at the same level form the ground, what must the initial magnitude of the velocity be if the rock is to hit the head just at the 98 yard tape? Give the answer in feet per second.

Answer 1

94.13 ft/s

Step-by-step explanation:

Given:

• 
  `t` = time interval in which the rock hits the opponent = 10 s - 5 s = 5 s

• 
  `s` = distance to be moved by the rock long the horizontal = 98 yards

• 
  `y` = displacement to be moved by the rock during the time of flight along the vertical = 0 yard

Assume:

• 
  `u` = magnitude of initial velocity of the rock

• 
  `\theta` = angle of the initial velocity with the horizontal.

For the motion of the rock along the vertical during the time of flight, the rock has a constant acceleration in the vertically downward direction.

`\therefore y = u\sin \theta t +(1)/(2)(-g)t^2\\\Rightarrow 0 = u\sin \theta 5 +(1)/(2)(-9.8)* 5^2\\\Rightarrow u\sin \theta 5 =(1)/(2)(9.8)* 5^2......(1)\\`

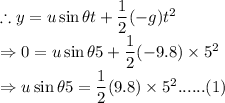
Now the rock has zero acceleration along the horizontal. This means it has a constant velocity along the horizontal during the time of flight.

`\therefore u\cos \theta t = s\\\Rightarrow u\cos \theta 5 = 98.....(2)\\`

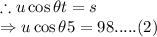
On dividing equation (1) by (2), we have

`\tan \theta = (25)/(20)\\\Rightarrow \tan \theta = 1.25\\\Rightarrow \theta = \tan^(-1)1.25\\\Rightarrow \theta = 51.34^\circ`

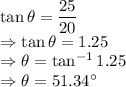
Now, putting this value in equation (2), we have

`u\cos 51.34^\circ*  5 = 98\\\Rightarrow u = (98)/(5\cos 51.34^\circ)\\\Rightarrow u =31.38\ yard/s\\\Rightarrow u =31.38* 3\ ft/s\\\Rightarrow u =94.13\ ft/s`

Hence, the initial velocity of the rock must a magnitude of 94.13 ft/s to hit the opponent exactly at 98 yards.