Question

A commuter train travels between two downtown stations. Because the stations are only 1.48 km apart, the train never reaches its maximum possible cruising speed. During rush hour the engineer minimizes the travel interval Δt between the two stations by accelerating for a time interval Δt1 at a1 = 0.100 m/s2 and then immediately braking with acceleration a2 = -0.510 m/s2 for a time interval Δt2. Find the minimum time interval of travel Δt and the time interval Δt1.

Answer 1

Δt=6.43h

Δt1 = 5.38h

Step-by-step explanation:

We know that the train has to stop at the destination, so in the interval Δt2:

Vf = Vo + a2*Δt2 where Vo is the final velocity in the intervat Δt1.

Vf = a1*Δt1 + a2*Δt2 = 0 Solving for Δt2:

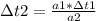`\Delta t2 = (a1*\Delta t1)/(a2)` Let this be eq1.

The total distance is 1.48km, and this is the sum of the displacements during Δt1 and Δt2:

`\Delta X = \Delta X1 + \Delta X2 = (a1*\Delta t1^2)/(2) + (a1*\Delta t1)*\Delta t2+(a2*\Delta t2^2)/(2)`

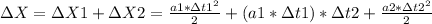
Replacing our previous value for Δt2 in this equation we can solve for Δt1:

Δt1 = 19351.36s ≅ 5.38h Using this value in eq1, we get Δt2:

Δt2 = 3794.39s ≅ 1.054h Therefore, total time Δt= 23145.75s ≅ 6.43h