Question

Whats 100 divided by 0.305 can you do it with work to please and 7 divided by 19.551

Answer 1

20000/61

1000/2793

this is the answers. i dont really know how to show my work

Answer 2

`\displaystyle(100)/(0.305) = 327.868852`

`\displaystyle(7)/(19.551) = 0.358037`

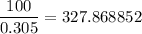
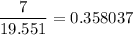
Explanation:

We have to find 100 divided by 0.305. This can be written as:

`\displaystyle(100)/(0.305)\\\\= \displaystyle(100* 1000)/(0.305* 1000)\\\\= \displaystyle(100000)/(305) = 327\displaystyle(53)/(61)`

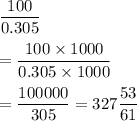
Reducing this fraction in lowest form by dividing the numerator and denominator by 5, we have,

`\displaystyle(20000)/(61)`

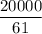
The decimal expansion of this fraction is 327.868852

Now, we have to divide 7 by 19.551. This can be written as:

`\displaystyle(7)/(19.551)\\\\= \displaystyle(7* 1000)/(19.551* 1000)\\\\= \displaystyle(7000)/(19551)`

Reducing this fraction in lowest form by dividing the numerator and denominator by 7, we have,

`\displaystyle(1000)/(2793)`

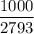
The decimal expansion of this fraction is 0.358037