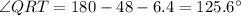Question

12. Find the measure of each interior angle of triangle QRT.

Answer 1

`\angle QRT=125.6\°`

`\angle RTQ=6.4\°`

`\angle TQR=48\°`

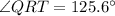
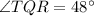
Explanation:

It is important to remember that, by definition, the measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles.

In this case we can idenfity that the angle
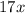`17x` is an exterior angle of the triangle QRT. Then:

`17x=\angle RTQ+\angle TQR`

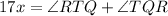
Where:

`\angle RTQ=2x\\\\\angle TQR=48\°`

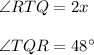
Substituting values and solving for "x", we get:

`17x=2x+48\\\\17x-2x=48\\\\15x=48\\\\x=3.2`

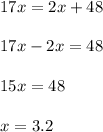
Then:

`17x=17(3.2)=54.4\°\\\\\\\angle RTQ=2(3.2)=6.4\°`

The sum of the interior angles of a triangle is 180°, therefore:

`\angle QRT+\angle RTQ+\angle TQR=180`

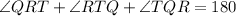
Solving for
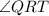`\angle QRT`, we get:

`\angle QRT=180-48-6.4=125.6\°`