Question

Vector A with arrow has a magnitude of 64 units and points due west, while vector B with arrow has the same magnitude and points due south. Specify the direction relative to due west.

Find the magnitude and direction of A with arrow and B with arrow.

Answer 1

The magnitude is 90.5.

The direction of
`(\vec{A}+ \vec{B})` is 45° south of west.

The direction of
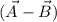`(\vec{A} - \vec{B})` is 45° north of west.

Explanation:

Let suppose the direction of unit vector as follows:

`\hat{i}` in the eastern direction

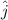`\hat{j}` in the northern direction

Given:

Vector A with arrow has a magnitude of 64 units and points due west, while vector B with arrow has the same magnitude and points due south.

Therefore,

`\vec{A} = -64 \hat{i}`

`|\vec{A}| = 64`

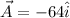
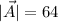
And

`\vec{B} = -64 \hat{j}`

`|\vec{B}| = 64`

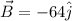
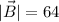
Formula used:

`The\ magnitude\ of\ vector\ (\vec{A}+ \vec{B}) = \sqrtA`

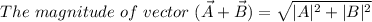
And the direction is given by:

`tan\theta = (|A|)/(|B|)`

Now,

The magnitude of
`(\vec{A}+ \vec{B})`:

`= \sqrt`

`= \sqrt{64^(2)+64^(2)}`

`= 64√(2)`

`= 90.5`

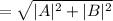
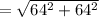
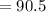
∴ The magnitude is 90.5.

And,

The direction relative to west is

`tan\theta = (|A|)/(|B|)`

θ = tan⁻¹ (B/A) = tan⁻¹ (64/64) = tan⁻¹ 1 = 45° south of west

∴ The direction is 45° south of west.

Again,

The magnitude of
`(\vec{A} - \vec{B})`:

`= \sqrt^(2)+`

`= \sqrt{64^(2)+64^(2)}`

`= 64√(2)`

`= 90.5`

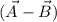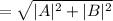
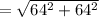
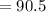
∴ The magnitude is 90.5.

And,

The direction relative to west is

`tan\theta = (|A|)/(|B|)`

θ = tan⁻¹ (B/A) = tan⁻¹ (64/64) = tan⁻¹ 1 = 45° north of west.

∴ The direction is 45° north of west.