Question

Box A contains 1 black and 3 white marbles, and box B contains 2 black and 4 white marbles. A box is selected at random, then a marble is drawn at random from the selected box. Given that the marble is black, find the probability that Box A was chosen.

Answer 1

Answer: Probability that Box A was chosen given that black marble is chosen is 0.5.

Explanation:

Since we have given that

Number of boxes = 2

In Box A,

Number of black marbles = 1

Number of white marbles = 3

In Box B,

Number of black marbles = 2

Number of white marbles = 4

Since black marble is selected.

So, using Bayes theorem , we get that

`P(E_1|B)}=(P(E_1).P(B|E_1))/(P(E_1).P(B|E_1)+P(E_2).P(E_2|B))\\\\P(E_1|B)=(0.5* (1)/(3))/(0.5(1)/(3)+0.5* (2)/(6))\\\\P(E_1|B)}=(0.167)/(0.167+0.167)\\\\P(E_1|B)}=0.5`

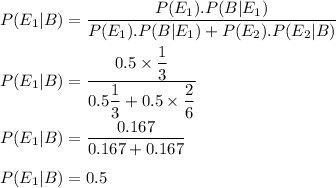
Hence, probability that Box A was chosen given that black marble is chosen is 0.5.