Question

Mr .Baker has baked some muffins. If he packs them in boxes of 4, he will have 3 left over. If he packs them in boxes of 5, he will also have 3 left over.If he packs them in boxes of 6, he will only have 1 left over. Find the least possible number of muffins Mr. Baker has baked.

Answer 1

`\boxed{43}`

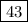
Explanation:

I think the easiest way to solve this problem is by brute force: trial and error.

We must find numbers that when divided by

• 4 leave 3 (4n + 3)
• 5 leave 3 (5n + 3)
• 6 leave 1 (6n + 1)

Here is a list of multiples of the integer n that satisfy the three conditions.
`\begin{array}c\mathbf{n} & \mathbf{4n+ 3} & \mathbf{5n + 3} & \mathbf{6n + 1}\\1 & 7 & 8 & 7\\2 & 11 & 13 & 13\\3 & 15 & 18 & 19\\4 & 19 & 23 & 25\\5 & 23 & 28 & 31\\6 & 27 & 33 & 37\\7 & 31 & 38 & \mathbf{43}\\8 & 35 & \mathbf{43} & 49\\9 & 39 & 48 & 55\\10 & \mathbf{43} & 53 & 61\\\end{array}\\\text{The only number that is common to all three lists is $\mathbf{43}$.}\\\text{The smallest possible number of muffins Mr. Baker could have baked is $\boxed{\mathbf{43}}$.}`

Check:

`43 / 4 = 10R3\\43 /5 = 8R3\\43 / 6 = 7R1`

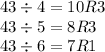
OK .