Question

John runs a computer software store. Yesterday he counted 121 people who walked by the store, 66 of whom came into the store. Of the 66, only 25 bought something in the store. (Round your answers to two decimal places.) (a) Estimate the probability that a person who walks by the store will enter the store. .55 Correct: Your answer is correct. (b) Estimate the probability that a person who walks into the store will buy something. .38 Correct: Your answer is correct. (c) Estimate the probability that a person who walks by the store will come in and buy something. Incorrect: Your answer is incorrect. (d) Estimate the probability that a person who comes into the store will buy nothing. .62 Correct: Your answer is correct.

Answer 1

a) There is a 55% probability that a person who walks by the store will enter the store.

b) There is a 38% probability that a person who walks into the store will buy something.

c) There is a 21% probability that a person who walks by the store will come in and buy something.

d) There is a 62% probability that a person who comes into the store will buy nothing.

Explanation:

This a probability problem.

The probability formula is given by:

`P = (D)/(T)`

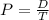
In which P is the probability, D is the number of desired outcomes and T is the number of total outcomes.

The problem states that:

121 people walked by the store.

66 people came into the store.

25 bought something in the store.

(a) Estimate the probability that a person who walks by the store will enter the store.

121 people walked by the store, 66 of whom entered the store. So:

`D = 66, T = 121`

`P = (D)/(T) = (66)/(121) = 0.55`

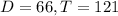
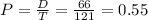
There is a 55% probability that a person who walks by the store will enter the store.

(b) Estimate the probability that a person who walks into the store will buy something.

66 people walked into the store, 25 of whom bought something. So:

`D = 25, T = 66`

`P = (D)/(T) = (25)/(66) = 0.38`

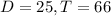
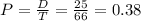
There is a 38% probability that a person who walks into the store will buy something.

(c) Estimate the probability that a person who walks by the store will come in and buy something.

121 people walked by the store, 25 of whom entered the store. So:

`D = 25, T = 121`

`P = (D)/(T) = (25)/(121) = 0.21`

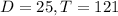
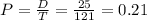
There is a 21% probability that a person who walks by the store will come in and buy something.

(d) Estimate the probability that a person who comes into the store will buy nothing.

Of the 66 people whom came into the store, 25 bought something. This means that 66-25 = 41 of them did not buy anything. So:

`D = 41, T = 66`

`P = (D)/(T) = (41)/(66) = 0.62`

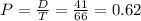
There is a 62% probability that a person who comes into the store will buy nothing.