Answer:
(D).
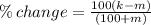
Explanation:
In the question,
Let us say the Price per Share, initially = 100x
and,
Earnings per Share = 100y
So,
Percent increase in Price per share = k%
Percent increase in Earning per share = m%
So,
New Price per Share = 100x + kx = (100 + k)x
and,
New Earnings per Share = 100y + my = (100 + m)y
Now,
Initial ratio of Price per Share to Earnings per share = 100x/100y = x/y
And,
Final ratio of Price per Share to Earning per share is,
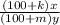
Now,
Percent increase in the ratio of Price per share to Earnings per share is,
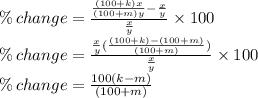
Therefore, the correct option is (D).