Answer:
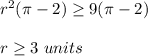
Explanation:
Find the area of the shaded region in terms of r.
1. The area of the circle with radius r is
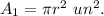
2. The area of the square with diagonal 2r is
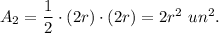
3. The area of the shaded region is the difference
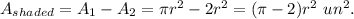
Since the area of the shaded region must be greater or equal to
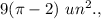 then
then
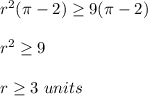
This inequality is solved only in positive numbers, because r cannot be negative.