Question

A 1.05-L bulb and a 1.52-L bulb are connected by a stopcock and filled, respectively, with argon at 0.72 atm and helium at 1.08 atm at the same temperature. Calculate the total pressure, the partial pressures of each gas, and the mole fraction of each gas after the stopcock has been opened. Assume ideal-gas behavior. (Answer in 3 significant figures)

Answer 1

Step-by-step explanation:

We have given that A 1.05-L bulb and a 1.52-L bulb are connected by a stopcock and filled with argon at 0.72 atm and helium at 1.08 atm respectively, at the same temperature.

Let P₁(p) be the partial pressure of gas in bulb A then

`P_1(p) * (1.05 + 1.52) = P_1V_1 = 1.05 * 0.72`

`P_1(p) = \frac {1.05}{2.57}* 0.72 = 0.294\ atm`

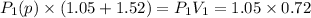
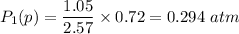
Similarly, Let
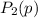`P_2(p)` be the partial pressure of gas in bulb B then

`P_2(p)* (1.05 +1.52) = P_2V_2 = 1.52 * 1.08\\\\P_2 (p) = \frac {1.52 * 1.08}{2.57} = 0.638\ atm`

Total pressure= 0.294 + 0.638 = 0.932atm

If n₁ and n₂ be their moles in the respective bulbs

P₁V₁ = n₁ R t

P₂ V₂ = n₂ R t

Now,

`\frac {P_1} {P_2} = \frac {n_1}{n_2}`

`(n_1)/(n_2+n_1 ) = (P_1V_1)/(P_1V_1+P_2V_2)`

`\text{mole fraction of argon} = (0.72* 1.05)/(0.72* 1.05+1.08*1.52) = \frac {0.756}{0.756 + 1.6416} \\\\\text{mole fraction of argon} = \frac {0.756}{2.3976} = 0.316`

`\text{Mole fraction of helium} = (1.08* 1.52)/(0.72* 1.05+1.08*1.52) = \frac {1.6416}{0.756 + 1.6416} \\\\\text{mole fraction of helium} = \frac {1.6416}{2.3976} = 0.6846`

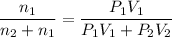
Mole fraction of argon = 0.316

Mole fraction of helium = 0.685