Question

The distribution of the amount of money spent by students on textbooks in a semester is approximately normal in shape with a mean of: μ = 455 and a standard deviation of: σ = 34. According to the standard deviation rule, almost 2.5% of the students spent more than what amount of money on textbooks in a semester?

Answer 1

523

Explanation:

We should calculate
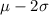`\mu-2\sigma` and
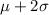`\mu+2\sigma`, i.e., we should calculate 455-2(34) and 455+2(34), doing the computations we find the following interval

(387, 523). According to the standard deviation rule 95% of the observations fall inside this interval, then, 5% of the data fall outside this interval, this because the distribution of the data is approximately normal. The normal distribution is symmetric, so, we have that 2.5% of the observations fall below 387 and 2.5% of the data fall above 523. Therefore 2.5% of the students spent more than 523.