Question

You have two biased coins. Coin A comes up heads with probability 0.1. Coin B comes up heads with probability 0.6.However, you are not sure which is which, so you choose a coin randomly and flip it. If the flip is heads, you guess that the flipped coin is B. Otherwise, you guess that the flipped coin is A.What is the probability that your guess is correct?

Answer 1

The probability that our guess is correct = 0.857.

Explanation:

The given question is based on A Conditional Probability with Biased Coins.

Given data:

P(Head | A) = 0.1

P(Head | B) = 0.6

By using Bayes' theorem:

`P(B|Head) = P(Head|B) * (P(B))/(P(Head))`

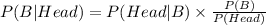
We know that P(B) = 0.5 = P(A), because coins A and B are equally likely to be picked.

Now,

P(Head) = P(A) × P(head | A) + P(B) × P(Head | B)

By putting the value, we get

P(Head) = 0.5 × 0.1 + 0.5 × 0.6

P(Head) = 0.35

Now put this value in
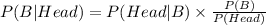`P(B|Head) = P(Head|B) * (P(B))/(P(Head))` , we get

`P(B|Head) = P(Head|B) * (P(B))/(P(Head))`

`P(B|Head) = 0.6 * (0.5)/(0.35)`

`P(B|Head) = 0.857`

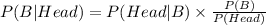
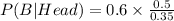
Similarly.

`P(A|Head) = 0.857`

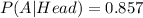
Hence, the probability that our guess is correct = 0.857.