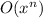Question

Fine the smallest positive integer n so that

f(x) = x^8 * log(x^3) + x^6 * log(x^5)

is a big-O of x^n

Answer 1

n = 9

Explanation:

Let's first prove that for any constants k > 0,
`n\geq 1`

`\lim_(x\to \infty)(\log x^k)/(x^n)=0`

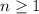
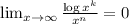
The derivative

`(\log (x^k))'=(kx^(k-1))/(x^k)=(k)/(x)`

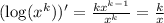
and the derivative
`(x^n)' = nx^(n-1)`

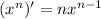
Now, applying L'Hôpital's rule we find that

`\lim_(x\to \infty)(\log x^k)/(x)=\lim_(x\to \infty)(k)/(nx^n)=0`

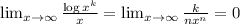
Now, let f be the function

`f(x)=x^8log(x^3)+x^6log(x^5)`

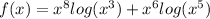
It is easy to see that f(x) is
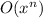`O(x^n)` only if
`n\geq 9`

If
`n\geq 9`

`(f(x))/(x^n)=(x^8log(x^3)+x^6log(x^5))/(x^n)=(log(x^3))/(x^(n-8))+(log(x^5))/(x^(n-6))`

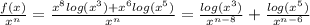
but both n-8 and n-6 are greater than one, so

`\lim_(x \to \infty)(f(x))/(x^n)=0`

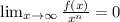
and f is
`O(x^n)`

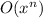
On the other hand, if
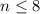`n \leq 8` then

`(f(x))/(x^n)=x^(8-n)log(x^3)+x^(6-n)log(x^5)`

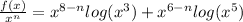
but 8-n is greater or equal than one, so

`\lim_(x \to \infty)(f(x))/(x^n)=\infty`

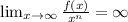
and so f(x) in not
`O(x^n)`