Question

An All-Pro defensive lineman is in contract negotiations. The team has offered the following salary structure: Time Salary 0 $ 5,700,000 1 4,300,000 2 4,800,000 3 5,300,000 4 6,700,000 5 7,400,000 6 8,200,000 All salaries are to be paid in a lump sum. The player has asked you as his agent to renegotiate the terms. He wants a $9.2 million signing bonus payable today and a contract value increase of $1,200,000. He also wants an equal salary paid every three months, with the first paycheck three months from now. If the discount rate is 4.7 percent compounded daily, what is the amount of his quarterly check? Assume 365 days in a year. (Do not round intermediate calculations and enter your answer in dollars, not millions of dollars, rounded to 2 decimal places, e.g., 1,234,567.89.)

Answer 1

PTM $ 1,225,900.379

Step-by-step explanation:

We will calculate the present value of the contract.

Then we will increase by 1,200,000

Next, we subtract the 9.2 bonus payable today

and distribute the rest under quarter payments:

We use present value of a lump sum

`(Nominal)/((1 + rate)^(time) ) = PV`

0 5,700,000 5,700,000

1 4,300,000 4,102,588.223

2 4,800,000 4,369,383.7

3 5,300,000 4,603,035.135

4 6,700,000 5,551,785.732

5 7,400,000 5,850,312.795

6 8,200,000 6,185,156.501

Then we add them: 36,362,262.09

We increase by 1,200,000

and subtract the 9,200,000 initial payment

28,362,262.09

this is the present value fothe quarterly payment

Next we calculate the equivalent compound rate per quarter:

`(1+(0.047)/(365) )^(365)  = (1+(r_e)/(4) )^(4) \\r_e = (\sqrt[4]{1+(0.047)/(365) )^(365)} - 1)* 4`

equivalent rate: 0.002954634

Now we claculate the PTM of an annuity of 24 quearter at this rate:

`PV / (1-(1+r)^(-time) )/(rate) = PTM\\`

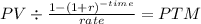
PV $28,362,262.09

time 24

rate 0.002954634

`28362262.0861625 * (1-(1+0.00295463425906195)^(-24) )/(0.00295463425906195) = PTM\\`

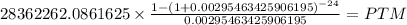
PTM $ 1,225,900.379