Question

A particle that is moving along a straight line accelerates from 40 cm/s to 20 cm/s in 5.0 s and then has a constant acceleration of 20 cm/s^2 during the next 4.0 s. The average speed over the entire time interval is _______.

Answer 1

Average speed,
`v_(avg)=43.33\ \rm cm/s`

Step-by-step explanation:

Given:

• Initial speed, u=40 cm/s
• final speed , v=20 cm/s
• Time taken, t=5 s

First case

Using equation of motion we have

`2as=v^2-u^2\\2as=20^2-40^2\\as=-600\\`

Now using,

`v=u +at\\20=40+a*5\\a=-4\ \rm cm/s^2`

now putting the value of a in first equation we get

`s=150\ \rm cm`

Second case

Acceleration
`a=20\ \rm cm/s^2`

Time taken
`t=4\ \rm s`

using equation of motion in one Dimension we have

`s=ut+(at^2)/(2)\\\\s=20\ties 4+(20* 4^2)/(2)\\s=240\ \rm cm`

Average speed is equal to total distance travelled per unit total time taken

`v_(avg)=(150+240)/(5+4)\\v_(avg)=43.33\ \rm cm/s`

Answer 2

43.33 cm/s

Step-by-step explanation:

Assume:

• u = initial speed of the particle

• v = final speed of the particle

• a = constant acceleration of the particle

• t = time interval for the acceleration

• s = distance traveled in the straight time
• 
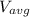  `V_(avg)` = average speed of the particle over the entire time interval

Case I

u = 40 cm/s

v = 20 cm/s

t = 5.0 s

Let us first calculate the acceleration of the particle in this time interval.

`a = (v-u)/(t)\\\Rightarrow a = (20-40)/(5)\\\Rightarrow a = -4\ cm/s^2`

Now, using the formula of displacement, we have

`s = ut+(1)/(2)at^2\\\Rightarrow s = (40)(5)+(1)/(2)* (-4)*(5)^2\\\Rightarrow s =150\ cm`

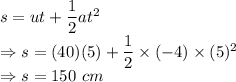
Since the particle does not change its direction during this time interval and it moves in a straight line. So, the displacement of the particle is equal to the distance traveled. This means the distance traveled by the particle in this time interval is 150 cm.

Case II

`a = 20\ cm/s^2\\t = 4.0\ s\\u = 20\ cm/s\\\therefore s = ut+(1)/(2)at^2\\\Rightarrow s = (20)(4)+(1)/(2)* (20)*(4)^2\\\Rightarrow s =240\ cm`

So, in this part, the distance traveled by the particle is 240 cm.

We know,

`\textrm{Average speed}=\frac{\textrm{Total distance }}{\textrm{Total time taken}}\\\Rightarrow V_(avg)=(150\ cm+240\ cm)/(5\ s+4\ s)\\\Rightarrow V_(avg)=43.33\ cm/s`

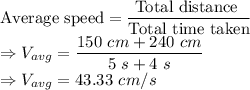
Hence, the average speed of the particle in the entire time interval is 43.33 cm/s.