Question

3. Find the perimeter of quadrilateral ABCD with vortices 4(-2,-2), B(-1,3),

c(5, 3), and D(4, -2).

Answer 1

`12 + 2 √(26)`

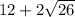
Explanation:

To find the perimeter of quadrilateral we need to calculate the length of its four sides which is distance between its four vertices.

where
`A(x_(1), y_(1)) = (-2, -2)`,

`B(x_(2), y_(2)) = (-1, 3)`

`C(x_(3), y_(3)) = (5, 3)`

`D(x_(4), y_(4)) = (4, -2)`

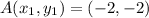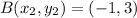
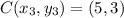
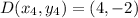
Distance of AB =
`\sqrt{\left (x^{_(2)}-x^{_(1)} \right )^(2)+\left (y_(2)-y_(1) \right )^(2)}`

=
`\sqrt{\left (-1+ 2 \right )^(2)+ (3 + 2)^{^(2)}}`

=
`\sqrt{1^{^(2)}+5^{^(2)}}`

=
`√(26)`

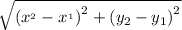
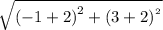
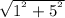
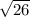
Distance of BC =
`\sqrt{\left (x_(3)-x_(2) \right )^(2)+ \left (y_(3)-y_(2)\right )^(2)}`

=
`\sqrt{(5+1)^(2)+ (3-3)^(2)} = √(36) = 6`

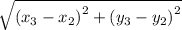
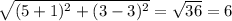
Distance of CD =
`\sqrt{\left (x_(4)-x_(3) \right )^(2)+ \left (y_(4)-y_(3)\right )^(2)`

=
`\sqrt{(4-5)^{^(2)}+(-2-3)^{^(2)}} = √(1 + 25) =√(26)`

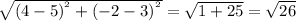
Distance of AD =
`\sqrt{\left (x_(4)-x_(1) \right )^(2)+ \left (y_(4)-y_(1) \right )^(2)`

=
`\sqrt{(4 + 2)^{_(2)}+ (-2 + 2)^{^(2)}}=√(36 + 0) = 6`

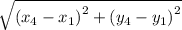
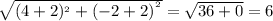
Perimeter of quadrilateral ABCD = Dist. ( AB + BC + CD + AD)

=
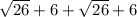
`√(26) +6 +√(26) +6`

=
`12 +2 √(26)`