Answer:
(a) 34.90 m/s
(b) 48.48 s
(c) 12 m/s
Step-by-step explanation:
Given:
- a = Maximum acceleration tolerable by the passengers =
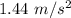
- x = distance between two stations = 846 m
- T = time of stoppage at each station = 22.0 s
- u = initial speed of the train = 0 m/s
For the maximum velocity attained by the subway train and also to stop at the destination (next station), the train must have to accelerate with a constant acceleration of
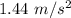 for half the journey to reach its maximum attainable velocity and then decelerate with
for half the journey to reach its maximum attainable velocity and then decelerate with
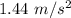 to stop at the next stage for the remaining half journey.
to stop at the next stage for the remaining half journey.
So, let us assume
- v = maximum speed of the train
- s = distance traveled to attain that maximum speed =
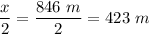
- t = time interval in which the maximum speed is attained
Part (a):
Using the equation for constant acceleration motion, we have
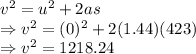
taking square root on both sides
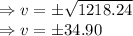
Since, speed of the train not be negative for the journey.

Hence, the train attains a maximum speed of 34.90 m/s between the two stations.
Part (b):
Let us first find out the time taken by the train to reach its maximum speed.
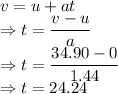
This means it takes 24.24 s to reach its maximum speed in the half journey.
Since the magnitude of acceleration and deceleration in both the half journey is the same. So, time taken by the train in both the journey will be the same.
So, the total travel time between the two stations is double the time travel in half the journey i.e., 48.48 s.
Hence, the travel time between stations is 48.48 s.
Part (c):
The train starts up from the originating one station and reaches the second station in the travel time (48.48 s) to wait for another 22.0 s at the destination. So, Total time = 48.48 s + 22.0 s = 70.48 s.
Now

Hence, the maximum average speed of the train from one start-up to the next is 12.0 m/s.