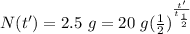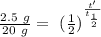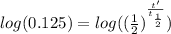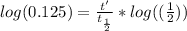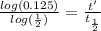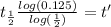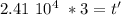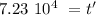Question

Now suppose you were using Plutonium 239 in a nuclear fission reactor. How long would it take 20 g of radioactive Plutonium 239 decay down to a safe 2.5 g? SHOW WORK.

Answer 1

It will take
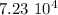`7.23 \ 10^4` years.

Step-by-step explanation:

Plutonium 239 has a half life of
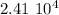`2.41 \ 10^4` years.

We know, for radioactive decay, that the quantity of radioactive material N at time t can be obtained with the equation

`N(t) = N_0 \  ((1)/(2))^{\frac{t}{t_{(1)/(2)}}}`

where
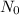`N_0` is the initial quantity of radioactive material and
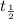`t_{(1)/(2)}` is the half life of the material.

Taking the values of our problem:

`N(t') = 2.5 \ g = 20 \ g \*  ((1)/(2))^{\frac{t'}{t_{(1)/(2)}}}`

`(2.5 \ g)/(20 \ g) =  \  ((1)/(2))^{\frac{t'}{t_{(1)/(2)}}}`

`log( 0.125) =    log(((1)/(2))^{\frac{t'}{t_{(1)/(2)}}} )`

`log( 0.125) =    {\frac{t'}{t_{(1)/(2)}}} * log(((1)/(2)) )`

`(log( 0.125))/(log((1)/(2))) =    \frac{t'}{t_{(1)/(2)}}}`

`t_{ (1)/(2) }  (log( 0.125))/(log((1)/(2))) =    t'`

`2.41 \ 10^4 \years\ * 3 =  t'`

`7.23 \ 10^4 \years\ =  t'`