Answer:
The three mistakes are:
1) Interchanging the variable x and y is incorrect.
2) Student need to use ± sign.
3) The domain of the function is incorrect it should be x ≤ 0.
Explanation:
Consider the provided steps.

Step 1:

The first step is wrong interchanging the variable x and y should be:
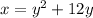
Step 2:
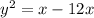
Step 3:
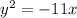
Step 4:
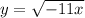 , for x≥0
, for x≥0
The step 4 is wrong because student need to use ± sign. The another mistake is the domain of the function is incorrect.
Because the radicand should be greater or equal to 0.
For which x must be less than or equal to zero. It should be x ≤ 0.