Question

(Score for Question 2: ___ of 5 points)

3. A line goes through the points (3,4) and (-3,6).
(a) What is the slope of the line? Show your work
(b) Write the equation of the line in point-slope form. Show your work
(c) Write the equation of the line in slope-intercept form. Show your work.
Answer:

Answer 1

Explanation:

a) Let's do this question by point-slope form, since we're given two coordinates, It's easier to use this method.

y-
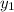`y_(1)` = m(x-
`x_(1)`)

6-4 = m(-3-2)

2=m(-5)

m= -2/5 Answer

b) It's easier since we solved the previous question with point slope form

y-4= -2/5 (x-3) Answer

c) y= mx + b (solve for the y-intercept)

4 = -2/5 (3) + b

4 + 6/5 = b

26/5 = b

Hence the equation is y = -2/5x+26/5 Answer

Hope this helps!

if you need clarifications anywhere, please let me know!

Answer 2

Explanation:

Let the points be
`\left ( x_1,y_1 \right )=\left ( 3,4 \right )\,,\,\left ( x_2,y_2 \right )=\left ( -3,6 \right )`.

(a) Slope of the line =
`(y_2-y_1)/(x_2-x_1)=(6-4)/(-3-3)=(2)/(-6)=(-1)/(3)`

(b) Let the slope be m.

From part (a), m =
`(-1)/(3)`

Point slope form is as follows:

`y-y_1=m(x-x_1)\\y-4=(-1)/(3)\left ( x-3 \right )`

(c) Slope intercept form is y = mx + b

where m is the slope of line and b is the y-intercept.

Here, m =
`(-1)/(3)`

To find : b

On putting
`\left ( x,y \right )=\left ( 3,4 \right )`, we get

`4=(-1)/(3)(3)+b\\4+1=b\\5=b`

So, slope intercept form is
`y=(-1)/(3)x+5`