Question

Software to detect fraud in consumer phone cards tracks the number of metropolitan areas where calls originate each day. It is found that 3% of the legitimate users originate calls from two or more metropolitan areas in a single day. However, 30% of fraudulent users originate calls from two or more metropolitan areas in a single day. The proportion of fraudulent users is 0.0131%. If the same user originates calls from two or more metropolitan areas in a single day, what is the probability that the user is fraudulent? Round your answer to six decimal places (e.g. 98.765432).

Answer 1

0.999987

Explanation:

Given that

The user is a legitimate one = E₁

The user is a fraudulent one = E₂

The same user originates calls from two metropolitan areas = A

Use Bay's Theorem to solve the problem

P(E₁) = 0.0131% = 0.000131

P(E₂) = 1 - P(E₁) = 0.999869

P(A/E₁) = 3% = 0.03

P(A/E₂) = 30% = 0.3

Given a randomly chosen user originates calls from two or more metropolitan, The probability that the user is fraudulent user is :

`P(E_2/A)=(P(E_2)* P(A/E_2))/(P(E_1)* P(A/E_1)+P(E_2)* P(A/E_2))`

`=((0.999869)(0.3))/((0.000131)(0.03)+(0.999869)(0.3))`

`(0.2999607)/(0.00000393+0.2999607)`

`(0.2999607)/(0.29996463)`

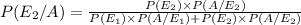
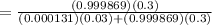
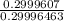
= 0.999986898 ≈ 0.999987