Answer:
a)
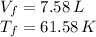
b)
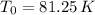
c):
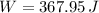
d)
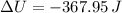
Step-by-step explanation:
We assume ideal gas behaviour (because of low pressure) and also that Argon has ideal monoatomic gas properties, namely:

For an adiabatic (constant entropy) process, we have for ideal gases that:
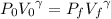
We can solve a) by solving for
 as follows:
as follows:
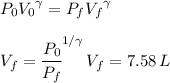
And we use the ideal gas law to get
 :
:
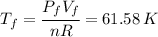
For b) we just have to apply the ideal gas law again:
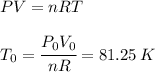
Where we have used:

For c), we can either integrate, or use the fact that the internal energy of am ideal gas depends only on its Temperature by:
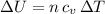
and thus:
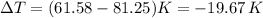
and so:
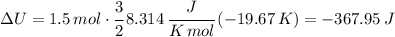
Which is the Answer to d), and we can then answer c) by the First law of thermodynamics:
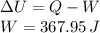
Where we have used the fact that the process is adiabatic, and thus no heat is exchanged between the system and its environment.