Question

To take off from the ground, an airplane must reach a sufficiently high speed. The velocity required for the takeoff, the takeoff velocity, depends on several factors, including the weight of the aircraft and the wind velocity.

A plane accelerates from rest at a constant rate of 5.00 m/s^2 along a runway that is 1800 m long. Assume that the plane reaches the required takeoff velocity at the end of the runway. What is the time t TO needed to take off?Express your answer in seconds using three significant figures.

Answer 1

The time needed to take off is
`t=26.8s`.

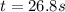Explanation: Let's order the information.

`x_i=0.00m`

`v_i=0.00(m)/(s)`

`a=5.00(m)/(s^2)`

`x_f=1800.00m`

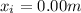
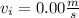
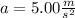
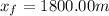
From Kinematics, the law for position as a function of time is:

`x(t)=x_i+v_it+(1)/(2)at^2`

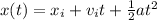
So the time needed to take off will fallow this rule:

`x_f=x_i+v_it+(1)/(2)at^2` ⇒
`(x_i-x_f)+v_it+(1)/(2)at^2=0`

⇒
`-x_f+(1)/(2)at^2=0` ⇒
`t=\sqrt{(2x_f)/(a) }`

∴
`t=\sqrt{(2x_f)/(a) }=26.83s`.

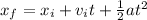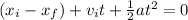
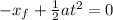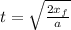
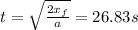This is the time needed to take off.

Written with only three significant figures:

`t=26.8s`.

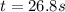Where the 8 stays the same since 3<5.