Answer:
friction factor is 0.01819
average speed v = 1.69 m/s
Reynolds number = 98786.7
and flow is turbulent
Step-by-step explanation:
given data
diameter d = 0.052 m
roughness ε=0.0015 mm
length l = 200 m
ΔP = 100 kPa
to find out
friction factor f, Reynolds number Re and average speed v
solution
we solve this by hit and try assume flow is turbulent
so we can say pipe flow
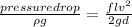 ...............1
...............1
here f is friction factor and l is length and d is diameter and ρ is density
so
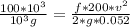
f v² = 0.052 ................2
we know Reynolds number =
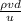
here u is viscosity of water that is 8.9 ×
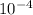
Reynolds number =
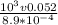
put here v from equation 2
Reynolds number =
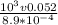 ×
×
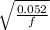
Reynolds number =
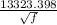 .................3
.................3
we know that 1/√f is
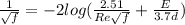
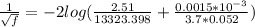
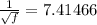
f = 0.01819
friction factor is 0.01819
and from equation 2
f v² = 0.052
0.01819 v² = 0.052
average speed v = 1.69 m/s
and from equation 3
Reynolds number =
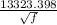
Reynolds number =
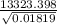
Reynolds number = 98786.7
so flow is turbulent