Answer:
Option 1.
Explanation:
The given equation is
![9^{(1)/(3)}=\sqrt[3]{9}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/yu55l277galo5s12qrrxhrazbefi75ddyw.png)
We need to find the equation which justifies the given equation.
Taking cube on both sides.
![(9^{(1)/(3)})^3=(\sqrt[3]{9})^3](https://img.qammunity.org/2020/formulas/mathematics/middle-school/w0s5repc12n7jkzji8pu0yjoc6ijr6x92c.png)
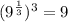
Taking LHS,
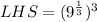
Using power property of exponents.
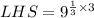
![[\because (a^m)^n=a^(mn)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/szk6cyxjbwli8sw7h22ardwfk55yjnha0d.png)

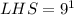
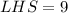

The required equation is
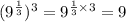
"Nine to the one third power all raised to the third power equals nine raised to the one third times three power equals nine".
Therefore, the correct option is 1.