Answer: 8
=========================================
Step-by-step explanation:
Through guess and check, we find that
8+9 = 17
8*9 = 72
We see that 8 is the answer.
--------------------
Another approach:
Let m and n be the two numbers.
They sum to 17 which leads to m+n = 17. Solving for n gets us n = -m+17.
Their product is 72, so, m*n = 72
Apply substitution and we get the following:
m*n = 72
m*(-m+17) = 72
-m^2 + 17m = 72
-m^2 + 17m - 72 = 0
-1(m^2 - 17m + 72) = 0
m^2 - 17m + 72 = 0
Now apply the quadratic formula
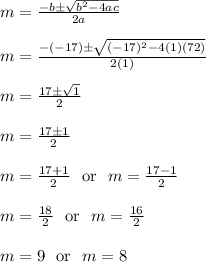
If m = 8, then n = -m+17 = -8+17 = 9.
If m = 9, then n = 8 through similar steps.
We see the two values are 8 and 9, the smaller of which is 8.