Answer:
a) The magnitud is 0.78m.
b) The direction is
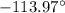 .
.
Step-by-step explanation:
Beetle 1 runs 0.41m due east, then 0.72m at
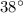 north of due east.
north of due east.
This means that it's vector position at the end for Beetle 1 is (in vector notation):
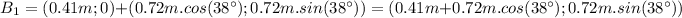
⇒
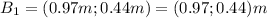
Beetle 2 first run is 1.74m at
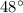 east of due north, this is:
east of due north, this is:
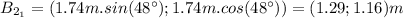
What's the difference between the final position of Beetle 1 and the position of the Beetle 2 after the first run? This difference will be the vector related to the second run of Beetle 2. This will be:
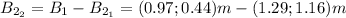
⇒
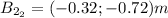
a) The magnitud the this second run will be:
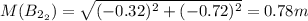 .
.
b) If
 is the direction of
is the direction of
![B_{2_(2)}[tex], we have:</p><p>[tex]tan(\theta )=(-0.72)/(-0.32)](https://img.qammunity.org/2020/formulas/physics/high-school/jc2t2nza6eakrp31fusu8mtkimg5oxlqi9.png) ⇒
⇒
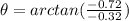 ⇒
⇒
 .
.
But from
 components we know the vector points out to the third quadrant (the angle gave of that value because signs canceled each other). The actual direction is
components we know the vector points out to the third quadrant (the angle gave of that value because signs canceled each other). The actual direction is
Ф=
 - 180° = -113.97°.
- 180° = -113.97°.