Question

Two loudspeakers are located 3.70 m apart on an outdoor stage. A listener is 18.7 m from one and 19.4 m from the other. During the sound check, a signal generator drives the two speakers in phase with the same amplitude and frequency. The transmitted frequency is swept through the audible range (20 Hz–20 kHz). The speed of sound in the air is 343 m/s. What are the three lowest frequencies that give minimum signal (destructive interference) at the listener's location?

Answer 1

The three lowest frequencies are 245 Hz, 730 Hz and 1225 Hz

Step-by-step explanation:

To get the frequencies, we need the formula for destructive interference

Δ
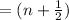`=(n+(1)/(2) )`*λ

where Δ is the path difference, λ is the wave lenght and n is number of the minimum we're looking for (n=0,1,2...). Then we can obtain the wave lenght for the thre first minimums.

`19.4m-18.7m=(0+(1)/(2))`*λ

λ=1.4m

`19.4m-18.7m=(1+(1)/(2))`*λ

λ=0.47m

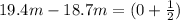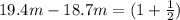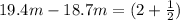`19.4m-18.7m=(2+(1)/(2))`*λ

λ=0.28m

Well, now using the formula for wave speed, we can get the frequencies for each minimum.

v=f*λ

where v is speed and f is frequency. We can solve now for the frequencies

`343m/s=f_(1) *1.4m\\f_(1)=245Hz\\\\343m/s=f_(2) *0.47m\\f_(2)=730Hz\\\\343m/s=f_(3) *0.28m\\f_(3)=1225Hz\\`