Question

A computer manufacturer built a new facility for assembling computers. There were construction and new equipment costs. The company paid for these costs and made combined profits of $40 million after 4 years, as shown in the graph:

There is a graph of a line with Years on the x axis and Profits in millions on the y axis that passes through 1, negative 50 and 4, 40.

Which equation most closely represents the line depicted in the graph?

f(x) = −30x + 80
f(x) = −40x + 4
f(x) = 40x − 4
f(x) = 30x − 80

Answer 1

f(x) = 30x − 80

Explanation:

Answer 2

f(x) = 30x − 80

Explanation:

The graph of the line passes through the following two points: (1, -50) and (4, 40). We have to find the equation of the line passing through these points.

In order to find the equation, we first need the slope of the line. The slope of the line is defined as:

`Slope=m=\frac{\text{Difference of y coordinates}}{\text{Difference of x coordinates}}`

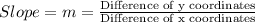
The first points in the ordered pair represent the x coordinates and the second points in each ordered pair represent the y - coordinates. Using these values in the above formula, we get:

`m=(40-(-50))/(4-1)=(90)/(3)=30`

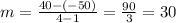
Thus, the slope of the line is m = 30.

The point slope form of the equation is:

`y-y_(1)=m(x-x_(1))`

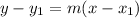
Using the point (4, 40) for (x1, y1) and the value of m, we get:

`y-40=30(x-4)\\\\ y-40=30x-120\\\\ y=30x-120+40\\\\ y=30x-80`

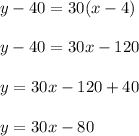
Thus, the equation representing the line depicted in the graph is f(x) = 30x - 80.