Question

im's uncle is 4 times as old as his nephew Jim. In 10 years, Jim's uncle age will be 20 years more than twice Jim's age. How old is Jim right now? Type a numerical answer in the space provided. for 17 points answer quick

Answer 1

15 years old.

Explanation:

Let Jim's age now be one unit (1u).

His uncle's age now is then 4 units.

Jim's age in 10 years = 1u + 10

Jim's uncle's age in 10 years = 4u + 10

In 10 years, Jim's uncle's age will be 20 years more than twice Jim's age.

Twice Jim's age =

`2(1u + 10) = 2u + 20`

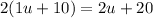
Since Jim's uncle's age is 20 years more than this, we can say that his uncle's age is equal to

`2u + 20 + 20`

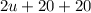
which is equal to

`2u + 40`

We found out that Jim's uncle's age in 10 years is 4u+10. Hence

`4u + 10 = 2u + 40`

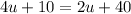
We subtract 10 from both sides:

`4u = 2u + 30`

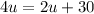
Therefore

`2u = 30`

and one unit is 15. Hence, Jim's age now is 15.