Answer:
See explanation below
Explanation:
Exponential growth (decay) is a way of describing the growth (decay) of a certain variable x (money, population, mass, etc..) with respect to time.
It happens when the speed of growth (decay) is proportional to the quantity itself at any given instant t.
If x(t) is the amount of the variable x at a certain instant t, the exponential growth (decay) can be modeled with the equation
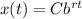
where C is the initial amount of x (when t=0) and its always considered positive, and b, r are constants that depends on the speed of growth (decay).
To find out if x(t) represents an exponential growth, check b and r.
If b > 1 AND r > 0 then x(t) represents an exponential growth. For example,
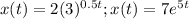
both represent exponential growth.
If r < 0 AND b >1 OR r > 0 AND 0 < b < 1 then it is an exponential decay. For example,
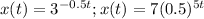
both represent exponential decay.