Question

points C,D, and E are collinear on CE, and CD:DE = 3/5. C is located at (1,8), D is located at (4,5), and E is located at (x,y). What are the values of x and y

Answer 1

The point E is located at (9,0)

x=9, y=0

Explanation:

we have that

Points C,D, and E are collinear on CE

Point D is between point C and point E

we know that

`CE=CD+DE` -----> equation A (by addition segment postulate)

`(CD)/(DE)=(3)/(5)`

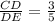
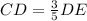`CD=(3)/(5)DE` ------> equation B

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

Find the distance CD

we have

C(1,8), D(4,5)

substitute in the formula

`CD=\sqrt{(5-8)^(2)+(4-1)^(2)}`

`CD=\sqrt{(-3)^(2)+(3)^(2)}`

`CD=√(18)\ units`

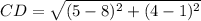
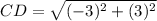
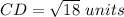
Find the distance DE

substitute the value of CD in the equation B and solve for DE

`√(18)=(3)/(5)DE`

`DE=(5√(18))/(3)\ units`

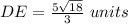
Find the distance CE

`CE=CD+DE`

we have

`DE=(5√(18))/(3)\ units`

`CD=√(18)\ units`

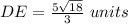
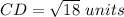
substitute the values in the equation A

`CE=√(18)+(5√(18))/(3)`

`CE=(8√(18))/(3)`

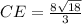
Applying the formula of distance CE

we have

`CE=(8√(18))/(3)`

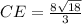
C(1,8), E(x,y)

substitute in the formula of distance

`(8√(18))/(3)=\sqrt{(y-8)^(2)+(x-1)^(2)}`

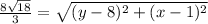
squared both sides

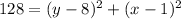`128=(y-8)^(2)+(x-1)^(2)` -----> equation C

Applying the formula of distance DE

we have

`DE=(5√(18))/(3)\ units`

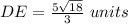
D(4,5), E(x,y)

substitute in the formula of distance

`(5√(18))/(3)=\sqrt{(y-5)^(2)+(x-4)^(2)}`

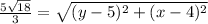
squared both sides

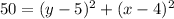`50=(y-5)^(2)+(x-4)^(2)` -----> equation D

we have the system

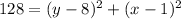`128=(y-8)^(2)+(x-1)^(2)` -----> equation C

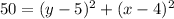`50=(y-5)^(2)+(x-4)^(2)` -----> equation D

Solve the system by graphing

The intersection point both graphs is the solution of the system

The solution is the point (9,0)

therefore

The point E is located at (9,0)

see the attached figure to better understand the problem