Answer:
92
Explanation:
Using the formula to calculate the average, and considering we know the result of the first 5 tests, we can calculate the score needed for the final exam in order to get an 80, using the following formula:
Average = (Sum of all the tests) / (number of tests)
where:
average = 80
x = score she needs to get for the final exam
number of tests = 6
Therefore,
80 =
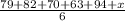
Finding a common denominator we have to multiply 80 by 6:
79 + 82 + 70 + 63 + 94 + x = 6*80
Adding the terms and multiplying:
388 + x = 480
So, x = 480 - 388
x = 92
Therefore, Brooke needs to get a 92 on her final exam in order to get an average score of 80.